Random Name Generator

The graphic on the right shows the 100 most common male names in America where the size of  each name is proportional to its popularity. The graphic is a ton more compelling as an interactive 3D document, but the picture conveys the main idea of how name popularity is distributed.

The difficulty in making an image like this, or anything like it really isn't in programming it. The program which was used to generate it is very simple. More difficult is acquiring the data.  In this case, I was able to acquire the data from Wolfram|Alpha in a computable format with very little work.

For exploratory programming, acquiring data to work with is probably one of the most important issues.  This is something not well addressed by most higher level programming languages. For them, the data which the code acts on is a secondary feature of the language rather than seen as an integral part of it.

Once I have access to the data, I am able to do a ton of difficult things that I would not normally be able to do. I can create a random name generator that returns realistic names back to me in the same proportion I would likely find them in the real world.

Despite the fact that the internet has brought us a ton of data to work with, finding what you want in a computable format is still very difficult.  Wasn't the semantic web supposed to fix that by assigning meaning to the data?

Random thoughts on design methods

 I've been thinking just now about how my style of programming has changed since going to college. My current work doesn't really lend itself to being called software engineering, but I do a fair amount of programming in it - usually in fairly small pieces. But even my programming outside of work has changed a bit.

I don't really create programs anymore. Programs are restricted in what they can do. I thought for a while that I was instead creating libraries for programming. After a while though, I realized that wasn't the case either. To a certain degree, I try to think about my packages as domain specific languages. I think about creating a way to write out common concepts I need to express and build the underlying functionality in a way that will be flexible. Only after doing this a ton do I begin actually writing the thing I want.

Maybe this is just something I never really got about programming before.

But I'm not sure what it is I am really understanding except the concept of a programming language is still underrated. 

MakeTurtle[] := Turtle[{0.,0.},0.,{}]; MakeTurtle[loc_,angle_,lines_]:=Turtle[loc,angle,lines];

Location[trtl_]:=trtl[[1]]; Angle[trtl_]:=trtl[[2]]; Lines[trtl_]:=trtl[[3]];

Move[trtl_,distance_]:=With[{newLoc = Location@trtl+distance*Cos[Angle@trtl],Sin[Angle@trtl]})},

MakeTurtle[newLoc,Angle@trtl,Append[Lines@trtl,Line[{Location@trtl,newLoc}]]]]

Move[distance_]:=Function[trtl,Move[trtl,distance]];

TurnRight[trtl_,angle_]:= MakeTurtle[Location@trtl,Angle@trtl+angle,Lines@trtl];

TurnRight[angle_]:=Function[trtl,TurnRight[trtl,angle]];

TurnLeft[trtl_,angle_]:= MakeTurtle[Location@trtl,Angle@trtl-angle,Lines@trtl];TurnLeft[angle_]:=Function[trtl,TurnLeft[trtl,angle]];

ShowTurtle[trtl_]:=Graphics@Lines@trtl;

trtl:=Nest[(#//TurnRight[RandomReal[{0,2Pi}]]//Move[RandomVariate[NormalDistribution[0,1]]])&,MakeTurtle[],300];

Some thoughts on usability of software and interfaces

 Usability seems to have a ton in common Huffman coding trees. If you are not familiar with them, take a look at the wikipedia article. Roughly speaking, a Huffman coding is a way of assigning smaller symbols to the most common elements of a signal and larger symbols to less common elements of a signal. By doing this, you can get a representation of the signal which is of a minimal size, the Huffman encoding.

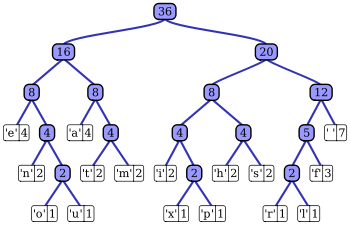A good programming language for example will be a lot like a Huffman encoding. The more common a task is, the easier it should be to accomplish in that programming language. There are, of course, forces pushing to make any programming language more verbose, such as readability and desire for specificity. But this at least offers a good explanation for why there should be so many programming languages - different languages are different codings for tasks we may wish to do. Novices to programming languages wonder why there is such a diversity of programming languages since to them it seems that there is a sharp cost in learning a new programming language and that all programming languages are essentially equivalent in power (Turing complete). They attribute the diversity of programming languages to either factionalism caused by corporations or the idea that progress has been made in the design of languages, which creates new languages while legacy ones remain to and require maintenance. There is of course truth in both of these. 

Not only does the Huffman code analogy help explain why there would be different languages for different areas, but it explains that some languages have different learning curves. By making it easy  to do common tasks, it necessarily makes it a bit harder to do less common tasks. Many programming languages seem hard then because they try to make a large set of tasks possible with them. Take for example spread sheet programs like Microsoft's Excel. They make it very easy to make graphs of data, but it is very difficult to get highly customized graphics. In fact, there are a large number of graphics which are basically impossible to make. Creating a simple graphic with a programming language like R, Python, or Mathematica though is more difficult than doing the same task with a spreadsheet. For this reason, people new to programming think that programming languages are needlessly difficult. However, when the graphs have to be customized in some way, they are likely to find they have much more freedom and can manage much more customization with a programming language than they could have with spreadsheet. In this way, programming languages resemble Huffman coding trees that are more well balanced than more task specific programs. 

The analogy with Huffman coding trees does not only extend to programming languages but other kinds of interfaces as well. Consider a simple user interface. If a certain task is more common, we can choose to make a button to perform that task more prominent than others perhaps by making it bigger or placing it at the top of a list. By doing this, we have made the other capabilities of the interface a bit harder to find. In this sense there is an encoding for the action and other actions have a longer encoding. 

Old Dog, New Trick

I've been using integration by parts lately to solve some unique problems. Unfortunately, it seems many people don't seem to think there is anything really interesting about it. I would like to show here a simple example of some of its more complicated things I've done with it recently.

First to start off with a quick definition of the integration by parts transformation.



This transformation is kinda useful for numerical integration as well. If you look at the right hand side, you'll see that a always appears integrated. For this reason, we can use this interpretation of the integral whenever the integral of a is better behaved than a itself.  Take this integral as an example:



This equation has no analytic solution and becomes very difficult to analyse numerically around 0. In fact a simple attempt to numerically integrate it won't give good results.

The oscillations are due to that problematic sine term. The amazing thing is how much better behaved the integral of sine(1/x) is than the original expression. The integral has an analytic solution in terms of  the Cosine Integral function: http://mathworld.wolfram.com/CosineIntegral.html. This function is not difficult to numerically approximate.

We can then make this integral easier to solve numerically by applying the integration by parts transformation. "a" here will be Sin(1/x) and "b" will be the exponential. First we compute the Integral of a. First I define the integral of the oscillating function:



Here Ci is the previously mentioned CosineIntegral function.  The full transformed integral is:



oI still oscillates, but not as widely as the previous function. This integral is easy to evaluate numerically. If we take out the analytic component and just focus on the integral, we can see we basically just transformed the function in the graph above into an analytically evaluable expression and the integral of this function:

I'm always kind of amazed what kinds of functions this technique can be applied to.

Some fun consequences of the previous post on Cauchy distributions

Look at my kinda rant on stack exchange here.

Essentially, the theory of diversification for stocks is completely different if you assume that the differentials of stocks are Cauchy distributed instead of Normally distributed. In fact, as I kinda point out, diversification doesn't even seem to make any sense under the conditions that stocks are levy processes.

There were a number of good answers and its gonna take me a while to go through the recommended reading.

Stocks are not Wiener Processes.

The controversy over the distribution that best fits the change of stock prices is apparently fairly recent. In turns out that stocks are actually Levy processes. I was stumbled across this fact while trying to fit the data onto the normal distribution and failing. Having read somewhere that the differential in stock prices is normal (see Black Sholes model), I assumed it would be at least a reasonable fit. After failing, I programmatically tried a ton of random distributions till a suitable fit was found.

Here is a histogram of the daily closing differences for General Electric. On top of it is superimposed a fit of the histogram with first the Normal distribution and then the Cauchy distribution. The fit was found using maximum likelihood estimation.

One of these is a better fit. Which do you think?

It blows my mind how terrible of a fit the Normal distribution is - why did it take Mandelbrot and Nassim Taleb to bring this fact up? In fact, running a simple test for normality on the data shows an incredibly small chance of it being normally distributed.

Of course this is not proof that the differential is Cauchy distributed. For that however you have to simply look at the properties of each distribution. For example the sum of two Cauchy random variables is another Cauchy random variable with parameters equal to the sum of the two previous parameters. Define beforehand the properties of stocks and you can derive the behavior of the distribution which should match it.

Using the normal distribution is fine if you are making some kind of approximation. However whenever an approximation is made, you have to ask how good it will be and under what conditions it fails. It looks like this hasn´t been seriously tried until recently.

For anyone who's lost their dog:

http://en.wikipedia.org/wiki/Epitaph_to_a_Dog

Analog Planimeter

I recently got one of these for my birthday:

http://www.math.ucsd.edu/~jeggers/Planimeter/KE_4242_1930/KE_4242_1930_gallery.html

It´s called a planimeter - a simple device which is used to calculate the area of an arbitrary blob. What is incredible is how simple the device is. At it's most basic, it is nothing more than two joined sticks and small wheel. It works because of Green's theorem, which is basically just the fundamental theorem of calculus (see post below). The fundamental theorem of calculus is everywhere. Mathematical!

The one I have is exactly like the one in the gallery above. It´s a 1930´s German manufactured planimeter. How did I come across this? About half a year ago, I was wandering in the beautiful stacks of the Math library at the University of Illinois. It might be one of the more interesting libraries around. The library is modeled on the throne room at Neushwarstein Castle of King Ludwig II of Bavaria, has dangerous translucent glass floors, and pictures of famous mathematicians whose gaze is at times very unnerving. The book collection isn't bad either. Although it is though a very small library by the university´s standards, they have a pile of books every month that they give away.

These days, the books are usually on some obscure branch of analysis and almost always in Cyrillic. I happened to find a book on the subject of Graphical and Mechanical Computation however.  This book was of practical use at the time of its publication, but the direction of our progress has made the techniques nothing more than curiosities. It's such a shame that progress has caused us to abandon such a beautiful technology. Fortunately, Google has preserved the book at the link above. I learned about the planimeter in some of the later chapters.

Maybe there is new interest in the subject. John D Cook recently reviewed this book on Nomology, a form of graphical numerical computation. I guess I have now another book to add to my shelf now...

Incarnations of the Fundamental Theorem of Calculus.

I'm not sure most people know how very often the fundamental theorem of calculus comes up. I'm  even more surprised how many people are hard pressed to be able to describe it, even if they work in a technical field were calculus is used.

The fundamental theorem of calculus basically says that deriving the rate of change of something and finding integrating the area are like ying/yang hot/cold addition/subtraction. They're complementary and undo each other.

Anyway, I'm writing this because I think I've stumbled across a kinda unintuitive result of it that shows how widespread this duality between area and rate is. I was looking at program written in Mathematica and came across the following snippet:

Mean@Differences@list

This code takes the mean of the differences of a list of numbers called list. The differences are simply the differences in the adjacent numbers: First minus Second, Second minus Third, and so on. The mean is just the average of them. The code here is inefficient. A small amount of algebra shows that there is a quicker way to compute this value than to take all of the differences and then take their means.

Let's say that our list of numbers is (a,b,c,d,e,f). Then our list of differences is (a-b,b-c,c-d,d-e,e-f). To average them, we add them all up and divide by the length of the list which is 6:

(a-b+b-c+c-d+d-e+e-f)/6

which is equal to (a-f)/6

It's not too hard to see. This result however is essentially just the fundamental theorem of calculus. This fact is not as clear - after all, there are no derivatives and integrals really used. They are discrete versions however and they are hidden in the actual problem.

First, the Differences function is a kind of discrete derivative. It is changing our list of numbers into a list of the rate of changes in the numbers. Rate of change is essentially just a derivative.

The second thing is that taking the mean of a set of numbers is kinda like integrating. In fact, most people will remember that you can take the average value of a continuous function by integrating it and dividing by the range over which you are averaging.

Putting these two together shows that they undo each other. The integral from a to z of a derivative is just the original function evaluated at a minus it evaluated at z. We divide by the length of the z-a to get the average.

Actually the correspondence between the difference operator and differentiation is kinda fun in general:

http://en.wikipedia.org/wiki/Difference_operator

Literature Reading Plan

First, the word "Plan" really shouldn't be here. In fact, I've chosen the title simply so I could I can write about  how my grand book reading plan is actually an un-plan. I don't want to give the impression that I've created a regime and book reading list based on the great authors. Instead, the plan is an emergent behavior - I read books I've bought by wandering around aimlessly at bookstores without any kind of timetable. I read books which are around me compulsively. This plan is a pattern which has emerged without intention in my life. 

The books aren't all things I have fun reading. In most cases, I would really prefer to be reading about math. There are a number of books on I've acquired by way of recommendation or I've prescribed to myself because I feel like they will be good for me.

I would have never been able to do this in college. Being compelled to read and lie about your views on one novel kills all of the energy needed to really read at least two or three of them. I'm amazed The

Here's a short list of the some of the types I've been reading over the past year:

Kurt Vonnegut

• TimeQuake
• Sirens of Titan

Like half of everything David Sedaris has written. "The Kid" by Dan Savage. 

Haruki Murakami

• Reread Underground
• Blind Willow, Sleeping Women
• Wind-up bird Chronicle

The Catcher in the Rye

and a bunch of others I've forgotten or didn't feel were worth any comment. Overall, this list is a bit more impressive than I would have thought it would be a year ago. 

I think Murakami and Vonnegut are a specific kind of reading for me. Reading abusrdist literature makes you more creative. It also probably makes you more likely to go insane, but the two are closely linked. 

The other identifiable trend in my reading is clearly gay literature. Savage's work is more centrally about being gay than Sedaris's comedy. Both however are fairly important to me for being gay works.  I feel like I could be easily criticized for being a gay guy reading gay literature for sake of being gay. 

gay gay gay gay gay gay gay 

However it is important to me to see a reflection of my life in literature. Growing up, I never saw people living out gay lives.  I know a number of people who would say that I shouldn't need media like TV, radio, and books to tell me how to live, but those people always had a reflection of their lives available to them wherever they wanted it. Maybe Asian Americans feel the same way to a degree reading Amy Tan. I feel like the need to be represented in literature is kind of universal. People who don't see their own troubles reflected in books likely are not reading. 

Some of my best reading recently

Cicero on the Cataline conspiracy:

http://www.bartleby.com/268/2/11.html

Julius Caesar on the Catiline conspiracy:

http://www.bartleby.com/268/2/19.html

Theo Jansen's Beasts

Dutch artist Theo Jansen has been selling miniature 3D printed reproductions of his work online from Shapeways. I got one last week. It's the only 3D printed plastic thing I own and strangely probably most futuristic thing I own. 3D printing is part of the future means of production and simply owning a piece of that is interesting enough.

http://www.shapeways.com/blog/archives/822-Theo-Jansens-3D-Printed-Strandbeests.html

The most interesting thing is how people react to it. People can't help but think of it as some kinda of animal-spider-pet. I've had several people demand to know what its name is. The object can't even move on its own and has no face or eyes, so this really surprised me. People seem to somehow relate to the object more than a robotic vacuum or one of those terrible robot puppies they sell at Christmastime.  Often people are just kinda freaked out about it. Its motion is pretty spider-like.

Two Techniques in Functional Programming in Mathematica

When I code for customers, I often end up using techniques of functional programming that  many people haven't seen before. This often ends up being problematic, and I've begun to identify the techniques I use that cause the most confusion and explain them when needed. Nevertheless, I use these in my own code because they help in creating well organized, readable code.

There are two techniques in particular that I find the most useful: decorators and closures.

Decorators
I use the term decorator very broadly. For this case, I define a decorator to be a function which takes in a function or a result and instead of using it as input for some other process causes some kind of side effect (it's not a very good definition, but will work here). In Python, decorators are used when defining a function, but I often use the term to apply to higher order functions I wrap around other functions which have some generic usage.  A basic example is a "deprecated" decorator. To test if a function is a decorator, remove it from your code. It shouldn't really affect the core computations of your program. Decorators aren't really aren't integral to a  program. They simply decorate. A decorator should also be modular -- it shouldn't  be built to work with a specific function, but should be able to be used generally across many different functions.

This example of a decorator is used to mark functions as having been deprecated.

deprecated[function_] := 
    Function[args, 
        Module[{}, Print["This function has been deprecated"]; 
        function[args]]
    ]

We can then simply use this when defining functions to give them a deprecation warning.

test = deprecated@
   Function[x, x + 1];

When test is ran now, it will warn that it is deprecated. The decorator could be used on pretty much any function definition. More advanced versions are possible. This version allows us to customize the deprecation message:

deprecated[replacement_?StringQ] :=  

    Function[function, Function[args,

        Module[{},

                            Print["This function has been replaced by "<> replacement];  
              function[args]]   
        ]]


Which can be used like:

test = deprecated["blarg"]@
   Function[x, x + 1];

test[1]

This function has been replaced by blarg

2 

Closures
Closures should be recognizable to anyone who knows functional programming. They provide a nice way to have state in a language without really explicitly mentioning state. Here is a really simple example in Mathematica:

 makeCounter[] := Module[{count = 0}, Function[{}, count++]];

counter = makeCounter[]; 

counter[]
1

counter[]
2
....

Counter is a function which has a state because it references a variable in its parent function makeCounter.  This is cleaner than creating a global variable to hold the global count. The value of counter can only be properly accessed by using counter as we have intended it. I can't give a full treatment of closures and their uses here, but I hope this gives a good idea of what they are.

Combining them
I've used the both closures and decorators together with great synergy in a number of tasks. For example, let's say we want a good way to keeping track of how many times certain functions have been called. We can make a closure which returns a pair: a function to be used as a decorator on functions which are to increment the counter and a function to access the value of the counter. For example:

makeCounterSystem[] := Module[{count = 0}   

    {Function[result, count++; result],Function[{}, count]}];

{counts, totalCount} = makeCounterSystem[];

counts@ Sin[RandomReal[]] ;

totalCount[]

1

This decorator here is different from the previous ones in that it decorates functions not where they are defined, but where they are ran. This can be modified to be a decorator on the definition of the function easily if needed. Whenever we call a function which has counts@ preppended to it, the count will incremented and can then be access by calling totalCount[].

There are numerous uses for this kind of combination. A common use is to keep a log of the results of a function silently:

makeLoggingSystem[] := Module[{log = {}},

  {Function[function, Function[args,  

                Module[{output=function[args]},

              AppendTo[log,output]; output]]],

           Function[{}, log]
     }
     ];

{logger, getLog} = makeLoggingSystem[];

test = logger@
   Function[x, N@Sin[x^2]];

Now whenever we call test, the resulting value is secretly logged and the entire history of the output of the function and any other function decorated by logger is accessible by running getLog[].

I am Bored

I am Bored

Everyday Life

This is taken from the a joke thread on stackexchange. I think I pretty much see this situation everyday.

A physicist, an engineer, and a statistician were out game hunting. The engineer spied a bear in the distance, so they got a little closer. "Let me take the first shot!" said the engineer, who missed the bear by three metres to the left. "You're incompetent! Let me try" insisted the physicist, who then proceeded to miss by three metres to the right. "Ooh, we got him!!" said the statistician.

Finding a Regression for a Circle

I was recently asked to fit a circle to a bunch of data points much like the one right here. You can see that the points are roughly distributed around in a circle of some kind. The task then is to find the equation of the circle which best fits this data.

The Problem

Fitting an equation to a set of data is not an uncommon problem. There´s a large amount of work done in algorithms for finding the ¨best¨ fit for many different definitions of ¨best¨. The person asking me to solve this problem was under the assumption that the normal method, least squares regression, was the best way of going about solving this problem. Actually, performing least squares regression in this case doesn´t really make any sense since the theory applies to only functions. Circles are not functions and so the theory doesn´t apply.

Despite this fact, there was a desire to stick with something like least square regression. I guess it´s like a brand name that people have come to trust. There was talk of some rather complicated solutions, like breaking up the circle into two branches and performing least squares regression on each half in some way, then averaging the results. Anyway you slice it, you´re coming up with an arbitrary algorithm for finding a fit for the function. So really you might as well come up with a sensible arbitrary algorithm.

The solution for the problem is in fact incredibly easy. If you understand what least squares regression is, then you would never attempt to use it for this kind of problem, or anything really remotely close to it.

I resolved the issue with two very clear ideas that cut the Gordian Knot:

•  The center of the circle is probably around the center of the points. 
• The radius of the circle is probably the average distance from the center.

The Simple Solution

This is what the end result is when you plot that circle with the data.  It´s probably pretty close to minimizing the absolute residual of the data against the function. The solution is perfect for what it needed to be used for and took about one line of clear Mathematica to program. Relying on math that you don´t understand often causes you to complicate otherwise simple problems.

Quantum Zombies

The idea the physics induces different kinds of computing must at this point be taken seriously. If were now looking at quantum entanglement in eyes of birds, then the idea that quantum mechanics might have a significant role in the physics of consciousness is not really that crazy of an idea.

As I believe I've pointed out earlier, besides being completely ridiculous by themselves, Kripke's arguments for qualia seems completely useless in the case of quantum consciousness. I wrote a big paper on this subject called "Quantum Zombies". I won't link to it here, since the paper itself is terrible.

Philosophers love to use the analogy of zombies to discuss consciousness. What you won't see in their discussion is any mention that intelligence might have some kind of quantum nature. Like the theory of computation did before, philosophers have assumed a kind of Newton model of physics when discussing these zombies. If their arguments are revisited knowing that the mechanics of thought might involve quantum mechanics, then their arguments about zombies stop making any kind of sense.

For example, Kripke suggests that it would be allowable that there could exist a perfect copy of a person. This copy would be a zombie copy. In a quantum model of thought, this idea of a copy would be ridiculous.

Design Versus Implementation

The process of software design is often broken up into software design and software implementation. Like all forms of organization and classification, it's inherently incorrect and misleading. It's also necessary for an intelligent conversation on software.

In many of the software projects I've worked on, there has been a tension between these two parts. Very often the roles are separated out and worked on separately, when in a deep sense they are inseparable. The separation of work into design and implementation, architect and foreman, brings about a great danger. If the architect doesn't understand the material and structures houses are built with and the foreman does not understand the purpose of the architect's design, not only will there be conflict, but a chance for holistic creativity is lost. Innovation often requires mastery of both halves.

In popular thought, business people are often guilty of this dilemma. There are many stories of business people who have an idea for the next great website. They only they need to get a programmer to implement their idea. All the hard work to them seems done. The business people are caught unaware of how software was made in practice and become frustrated. Not aware that software creation must be part of the creative process, their projects fail.

Directing programmers is difficult, because software design isn't problem solving. It is problem avoidance. You can ask a programmer to solve a problem, but very often instead she will find a way to avoid it all together. The path of least resistance is often the best and not the one the designer had in mind.

Insert Taoist quote here about how programmers are like water or something like that...
-Laozi

Many have gone so far as to completely discredit the design part of the process. Many stories about internet startups are about how they stumbled into their niche. All they had were quality team of programmers and software designers. They went where their code took them. To some degree this is true. The book, Do More Faster, suggests that ideas are much more worthless than people believe. This is the over arching theme of its first section. Despite the ridiculous name of the book, I recommend it.

The greatest master of both implementation and design might be Frank Llyod Wright. His writings about architecture stress the importance of knowing the whole process of construction. Wright devoted a large amount of his time to understanding the construction methods and materials of his houses and this reflected in his teaching. His college of architecture was known for making students do menial work like carpentry and even farming on top of standard architectural education. Ayn Rand's Howard Roark was a construction worker for much of The Fountainhead. His understanding of the building materials and construction techniques allowed him to innovate where his competing architect's ideas stagnated.

Japanese Wikipedia

Some things are just difficult to learn unless you´re in the correct setting. Japanese is a good example. A college classroom is okay for learning Japanese, and unfortunately better than what I can do right now. Studying abroad is the only way anyone ever seems to actually learn Japanese and I don´t think that will ever happen for me.

Since I no longer have the burden of college, or the luxury of the being forced to study, I´m at a bit of a loss as to how to maintain my Japanese. I know just enough to make forgetting things really easy, and not enough to make the skill actually useful right now. I didn´t touch Japanese for over 2 years between when I took it highschool and college. I take it as a credit to my character that I didn´t forget it and actually slightly improved over those 2 years.

I don´t know why I bother maintaining my Japanese now. What are the chances of me ever going to Japan? Unless I specifically move there or try to find a job there, I don´t see myself very likely using it. Maybe I like the challenge of learning to write more characters, but I find it hard to justify why I spend time on it. I´ve never been out of the country and hardly left the midwest of America. I didn´t make a choice never to travel. It just never happened.

My friends think this lack of travel experience is a huge problem. I find it hard to see why. Many of benefits of study abroad are things I already consider well within in my skill set. I´ve managed to have a good amount of culture shock here at home. I´ve had to actively seek it, but I have always found it. Despite my lack of first hand international experience, I am a fairly international kinda guy. To my friends though, my apathy to travel is nothing short of a sure sign of an underlying phobia.

Travel reminds me a Zen koan I read somewhere once. Went something like this:

A student once went to see his master. When the student arrived and found the master kept a pet bird in a cage. The student asked the master why they kept the bird caged when it should be free to go where it wanted. The master opened the cage and as the bird flew away asked, ¨and how will the bird escape this? ¨.

Don´t hold me to the authenticity of that Koan. I simply want to use it to illustrate my feeling on travel. I´m pretty sure no one will accept it as an explanation, but there it is.

Once I am in a new place, what will I do there thats different from here? That´s all that really matters to me. Traveling somewhere simply to escape the midwest isn´t really a good way to become free. Of course, this all might be the rationalization of someone who is afraid to travel.

I recently tried to use Skritter to learn Japanese. It´s not for me. I can hear my old Japanese teacher deploring how it doesn´t teach proper writing style. I personally feel like I should be able to study without it.

I recently decided I should read more Japanese Wikipedia. Even better, I should edit English Wikipedia to contain some of the information in Japanese Wikipedia. This would really help my ability to read and make me feel like I´m at least doing something productive (whether this is actually productive is a debate for later). I think that is something I can do and be happy with, even if it´s as close as I ever get to going to Japan.

Orthogonality

There are some overarching ideas from math that seem to make their way into my everyday life. Orthogonality is one of the newer ones. I've come to appreciate it more recently, seeing it in so many different aspects in so many different areas and applications.

Most engineers and scientists use the term to refer solely to vectors, while the use can be extended to many different types of mathematical objects. The idea however is a very broad one. Parts of code for example can be orthogonal. If changing one part doesn't affect the other parts, this is intuitively like orthogonal vectors. Part of good software design is then a kind of orthogonalization. ( My spell check keeps on warning me "orthogonalization" is technical jargon, but I can't seem to find a suitable expression for it in normal English. )

Analysis is best done by breaking a complicated thing into orthogonal components. This is often an assumed fact. It is clearly intuitive in linear algebra. It is not so clear when it comes to Legendre polynomials for example where it appears to a student that we are adding complexity to make orthogonality. It is not so clear that this makes the computation easier. The best example of the perils of poorly orthogonalized systems might come from statistical modeling in the form of Multicollinearity. A multicollinear model is nothing more than a statistical model whose variables are not well orthogonalized. Multicollinearity is an cause of poor statistical model design in the same way that strongly linked objects are a cause of poor program design.