Random Name Generator

The graphic on the right shows the 100 most common male names in America where the size of  each name is proportional to its popularity. The graphic is a ton more compelling as an interactive 3D document, but the picture conveys the main idea of how name popularity is distributed.

The difficulty in making an image like this, or anything like it really isn't in programming it. The program which was used to generate it is very simple. More difficult is acquiring the data.  In this case, I was able to acquire the data from Wolfram|Alpha in a computable format with very little work.

For exploratory programming, acquiring data to work with is probably one of the most important issues.  This is something not well addressed by most higher level programming languages. For them, the data which the code acts on is a secondary feature of the language rather than seen as an integral part of it.

Once I have access to the data, I am able to do a ton of difficult things that I would not normally be able to do. I can create a random name generator that returns realistic names back to me in the same proportion I would likely find them in the real world.

Despite the fact that the internet has brought us a ton of data to work with, finding what you want in a computable format is still very difficult.  Wasn't the semantic web supposed to fix that by assigning meaning to the data?

Random thoughts on design methods

 I've been thinking just now about how my style of programming has changed since going to college. My current work doesn't really lend itself to being called software engineering, but I do a fair amount of programming in it - usually in fairly small pieces. But even my programming outside of work has changed a bit.

I don't really create programs anymore. Programs are restricted in what they can do. I thought for a while that I was instead creating libraries for programming. After a while though, I realized that wasn't the case either. To a certain degree, I try to think about my packages as domain specific languages. I think about creating a way to write out common concepts I need to express and build the underlying functionality in a way that will be flexible. Only after doing this a ton do I begin actually writing the thing I want.

Maybe this is just something I never really got about programming before.

But I'm not sure what it is I am really understanding except the concept of a programming language is still underrated. 

MakeTurtle[] := Turtle[{0.,0.},0.,{}]; MakeTurtle[loc_,angle_,lines_]:=Turtle[loc,angle,lines];

Location[trtl_]:=trtl[[1]]; Angle[trtl_]:=trtl[[2]]; Lines[trtl_]:=trtl[[3]];

Move[trtl_,distance_]:=With[{newLoc = Location@trtl+distance*Cos[Angle@trtl],Sin[Angle@trtl]})},

MakeTurtle[newLoc,Angle@trtl,Append[Lines@trtl,Line[{Location@trtl,newLoc}]]]]

Move[distance_]:=Function[trtl,Move[trtl,distance]];

TurnRight[trtl_,angle_]:= MakeTurtle[Location@trtl,Angle@trtl+angle,Lines@trtl];

TurnRight[angle_]:=Function[trtl,TurnRight[trtl,angle]];

TurnLeft[trtl_,angle_]:= MakeTurtle[Location@trtl,Angle@trtl-angle,Lines@trtl];TurnLeft[angle_]:=Function[trtl,TurnLeft[trtl,angle]];

ShowTurtle[trtl_]:=Graphics@Lines@trtl;

trtl:=Nest[(#//TurnRight[RandomReal[{0,2Pi}]]//Move[RandomVariate[NormalDistribution[0,1]]])&,MakeTurtle[],300];

Some thoughts on usability of software and interfaces

 Usability seems to have a ton in common Huffman coding trees. If you are not familiar with them, take a look at the wikipedia article. Roughly speaking, a Huffman coding is a way of assigning smaller symbols to the most common elements of a signal and larger symbols to less common elements of a signal. By doing this, you can get a representation of the signal which is of a minimal size, the Huffman encoding.

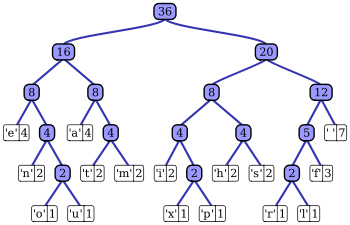A good programming language for example will be a lot like a Huffman encoding. The more common a task is, the easier it should be to accomplish in that programming language. There are, of course, forces pushing to make any programming language more verbose, such as readability and desire for specificity. But this at least offers a good explanation for why there should be so many programming languages - different languages are different codings for tasks we may wish to do. Novices to programming languages wonder why there is such a diversity of programming languages since to them it seems that there is a sharp cost in learning a new programming language and that all programming languages are essentially equivalent in power (Turing complete). They attribute the diversity of programming languages to either factionalism caused by corporations or the idea that progress has been made in the design of languages, which creates new languages while legacy ones remain to and require maintenance. There is of course truth in both of these. 

Not only does the Huffman code analogy help explain why there would be different languages for different areas, but it explains that some languages have different learning curves. By making it easy  to do common tasks, it necessarily makes it a bit harder to do less common tasks. Many programming languages seem hard then because they try to make a large set of tasks possible with them. Take for example spread sheet programs like Microsoft's Excel. They make it very easy to make graphs of data, but it is very difficult to get highly customized graphics. In fact, there are a large number of graphics which are basically impossible to make. Creating a simple graphic with a programming language like R, Python, or Mathematica though is more difficult than doing the same task with a spreadsheet. For this reason, people new to programming think that programming languages are needlessly difficult. However, when the graphs have to be customized in some way, they are likely to find they have much more freedom and can manage much more customization with a programming language than they could have with spreadsheet. In this way, programming languages resemble Huffman coding trees that are more well balanced than more task specific programs. 

The analogy with Huffman coding trees does not only extend to programming languages but other kinds of interfaces as well. Consider a simple user interface. If a certain task is more common, we can choose to make a button to perform that task more prominent than others perhaps by making it bigger or placing it at the top of a list. By doing this, we have made the other capabilities of the interface a bit harder to find. In this sense there is an encoding for the action and other actions have a longer encoding.